Zadatak za treći razred gimnazije Jingle bells, jingle bells, jingle all the way
Zadatak za treći razred gimnazije
Jingle bells, jingle bells, jingle all the way
Rok za predaju radova je 14. april. 2024.
Radove je potrebno poslati na hajdukovicgordana.nsad@s-markovic.edu.rs
Šta je zvuk?
Longitudinalni mehanički talas u vazduhu koji naš organ
sluha može da detektuje, a to je talas čija se frekvencija nalazi u intervalu
16Hz - 20000 Hz, naziva se zvuk. Ako je frekvencija ovih talasa niža od 16 Hz
oni se nazivaju infrazvuk, a ako je viša od 20 000 Hz nazivaju se ultrazvuk.
Mehanički talasi se prostiru kroz sredine u sva tri agregatna stanja. Ipak da
bi ih naš organ sluha detektovao, oscilacije koje izazivaju mehanički talasi
moraju biti prenesene na okolni vazduh. Stvaranje, prostiranje, apsorpciju i
odbijanje zvuka proučava nauka koja naziva se akustika.
Zvuk je longitudinalni mehanički talas u vazduhu čija se frekvencija
nalazi u intervalu 16 Hz – 20 000 Hz.
Postoje 3 vrste zvuka:
1. zvuk kao sredstvo komunikacije
2. zvuk kao alat (ultrazvučne dijagnostičke metode)
3. zvuk kao buka.
Zadatak 1.
Uz pomoć ređeg Oobleck-a (ređa
mešavina skroba i vode) je moguće zvučne talase pretvoriti u mehaničke i
vidljive talase. Ukoliko se Oobleck sipa na zvučnik, a preko nekog audio uređaja
ili ton generatora se podešava frekvencija zvuka, tada je moguće dodatno
objasniti pojam više i niže frekvencije, ali isto tako to i vizuelno pokazati.
Za izvođenje eksperimenta je potreban zvučnik, metalna tacna
i generator zvuka. Danas je vrlo jednostavno doći do programa koji generišu
zvuk tačno određene frekvencije (dostupno na internetu ili u aplikaciji
phyphox)
Pogledaj kako treba da izgleda na sledećem linku: http://www.youtube.com/watch?v=UU7iuJ98fRQ

Zadatak 2
Posmatrajmo normalan upad zvučnih talasa na graničnu
površinu iz ređe u gušću sredinu, npr. iz vazduha u tečnost ili čvrsto stanje.
Pošto su zvučni talasi longitudinalni, njihovo prostiranje kroz neku sredinu je
praćeno na pojedinim sabijanjem (kompresijom), a na drugim mestima istezanjem
(ekspanzijom) čestica sredine, tj. oscilacijama njene gustine. Radi toga,
kompresija ili ekspanzija ređe sredine na mestu upada talasa neće biti praćena
znatnijom deformacijom gušće sredine, te će kompresija ili ekspanzija ređe
sredine izazvana upadnim talasima biti praćena kompresijom ili ekspanzijom iste
sredine kod odbijenih talasa. To dovodi do toga, da pri odbijanju od gušće
sredine dolazi do promene faze talasa za fazni ugao π, dok pri prelasku talasa iz gušće u ređu
sredinu ne dolazi do promene faze. Talasna dužina, a time i frekvencija
talasa pri refleksiji ostaje nepromenjena, a amplituda se smanjuje.
Između upadnih i odbijenih talasa dolazi do pojave
interferencije, tako da će se oscilacije čestica sredine odvijati
shodno rezultujućem talasu. Interferencijom dva koherentna (stalne fazne
razlike i iste frekvencije) harmonijska talasa iste amplitude koji se kreću u
suprotnim smerovima duž istog pravca dolazi do karakterističnog talasnog
kretanja, nazvanog stojeći talas. Amplituda oscilovanja čestica
sredine u slučaju stojećih talasa menja se duž pravca njegovog prostiranja,
tako da postoje određena mesta koje nazivamo čvorovi gde nemamo nikakvog
oscilovanja, a između njih mesta nazvana trbusi stojećih talasa gde je
amplituda oscilovanja maksimalna. Pojava stojećih talasa može da nastupi i
prilikom refleksije na graničnoj površini sredina različitih gustina.
Posmatrajmo slučaj kada prilikom refleksije od gušće sredine
neznatan deo energije talasnog kretanja prelazi u drugu sredinu, tako da
direktni i reflektovani talasi imaju približno iste amplitude. Tada direktni
talas koji se prostire u pravcu x-ose možemo predstaviti jednačinom
Zbog promene faze za ugao π
i kretanja u suprotnom smeru, za reflektovani talas možemo pisati
Elongacija rezultujućih oscilacija na nekom mestu x i u
vremenu t se dobija zbirom ovih dveju
elongacija, tako da imamo
što predstavlja jednačinu stojećih talasa. Veličina –
2 y0 sinω![]() ne zavisi od vremena, nego od položaja
oscilacije čestice i predstavlja amplitudu stojećeg talasa, dok član cosωt pokazuje da čestice
sredine osciluju harmonijski u vremenu. Mesta gde nema oscilovanja (čvorovi
talasa) odgovaraju nultoj vrednosti amplitude stojećeg talasa, tj. kada je sinω
ne zavisi od vremena, nego od položaja
oscilacije čestice i predstavlja amplitudu stojećeg talasa, dok član cosωt pokazuje da čestice
sredine osciluju harmonijski u vremenu. Mesta gde nema oscilovanja (čvorovi
talasa) odgovaraju nultoj vrednosti amplitude stojećeg talasa, tj. kada je sinω![]() = 0. To će biti zadovoljeno u slučaju kada je
= 0. To će biti zadovoljeno u slučaju kada je
Lako zaključujemo da je rastojanje između dva susedna
čvora λ/2.
Na sličan način nalazimo položaj maksimalnog oscilovanja čestica (trbuha
talasa). U tom slučaju treba da bude sin ω![]() = 1, odakle dobijamo
= 1, odakle dobijamo
I rastojanje između susednih trbuha iznosi takođe λ/2.
Stojeći talas obično nastaje pri prostiranju zvučnih talasa
u sredinama ograničenih dimenzija, kod kojih može da dođe do višestrukog
odbijanja bez znatnijeg gubitka zvučne energije. Ako su dimenzije sredine u
kojoj se prostiru talasi takve da talas poslije dvostrukog odbijanja (od jedne
do druge granične površine sredine) dođe u fazu sa primarnim talasom (kada svi
talasi dolaze u čvor ili trbuh sa istom fazom), dolazi do najintenzivnijeg
oscilovanja čestica u trbusima stojećih talasa. Tada se zapaža izraženo povećanje
amplitude talasa na mestima trbuha, kao rezultat zvučne rezonancije.
Postupak merenja
Obzirom da je da je rastojanje između susednih čvorova i
trbuha stojećih talasa λ/4,
može se zaključiti da će uslov za pojavu zvučne rezonancije biti ispunjen
ukoliko je dužina vazdušnog stuba u cevi jednaka λ/4,
3λ/4, 5λ/4, . . ., ili u opštem
slučaju kada je ispunjen uslov
Ln=(2n+1)![]() (n = 0, 1, 2, 3, . . .).
(n = 0, 1, 2, 3, . . .).
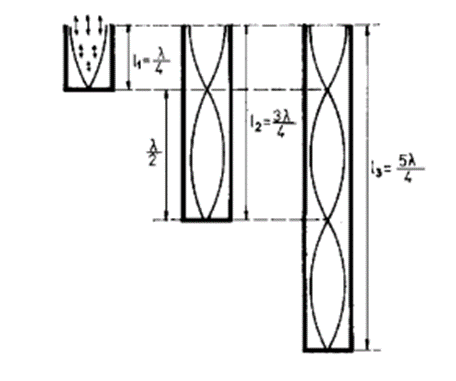
Tako se može formirati stojeći talas sa jednim, dva, ili
više čvorova u zavisnosti od odnosa dužine vazdušnog stuba u cevi i talasne
dužine zvučnih talasa. Ako se amplituda oscilacija čestica nanese normalno na
osu njihovih oscilacija, oblici stojećih talasa sa čvorovima i trbusima se mogu
shematski prikazati na crtežu:
Prinesemo li otvoru cevi neki zvučni izvor frekvencije ν, oscilovanje ovog izvora izaziva prinudno oscilovanje čestica vazdušnog stuba istom frekvencijom. Ukoliko je ispunjen uslov da je frekvencija tog zvučnog izvora jednaka rezonantnoj frekvenciji određenoj izrazom ν = c/λ, dolazi do rezonacije vazdušnog stuba praćenom znatnim pojačanjem intenziteta zvuka. Merenjem dužine stuba između dve susedne rezonancije, može se odrediti talasna dužina λ, a time na i frekvencija ν zvučnog izvora.
Procedura:
Odredi frekvenciju zvučnog talasa poštujući proceduru koja
je data u videu.
https://www.youtube.com/watch?v=aTqYc1w8h6M
Potrebno je:
1.
Realizovati od 3 do 5 merenja frekvencije (kao
što je prikazano)
2.
Izračunati srednju vrednost frekvencije
3.
Izračunati apsolutnu i relativnu grešku
4. Predstaviti rezultat merenja u obliku ν = νsr +/- Δν
Pitanja:
1.
Šta je zvuk? Kako smo podelili zvuk prema
frekvenciji?
2.
Gde se koriste pojedine vrste zvuka?
3.
Istraži koje frekvencije odgovaraju nekim
zvucima (sopran, bik, komarac…)
4.
Šta je ton, šta boja tona a šta oktava?
5.
Istraži kako se menja osetljivost ljudskog uha
po frekvencijama, za različite vrednosti glasnoće zvuka.
6.
Šta je stojeći talas?
7.
Šta je buka? U kojim jedinicama se izražava?
Koji je dozvoljeni nivo buke u životnoj sredini?
8.
Navedi izvore buke i koje posledice imaju na
organizam s obzirom na jačinu.
9.
Kako se zaštiti od buke u svom domu?
10.
Koje mere je potrebno preduzeti u cilju zaštite
i unapređenja životne sredine kako bi se eliminisali negativni efekti
savremenih uređaja na životnu sredinu.
11.
Kako se zvuk koristi u dijagnostičke svrhe?
Podsetimo se:
Rad treba da sadrži oba zadatka koja su data u uputstvu.
1. Izveštaj treba da
bude u vidu prezentacije ili dokumenta
2. Treba da sadrži pozadinsko
istraživanje, obrazloženje proučavanog problema, postavljeno pitanje, hipotezu,
rezultate predstavljene tabelarno, izračunate greške, predstavljen rezultat u
traženom obliku
3. Izveštaj treba da
sadrži sve fotografije i video zapis svih faza postupka
4. Zaključak i
odgovore na pitanja


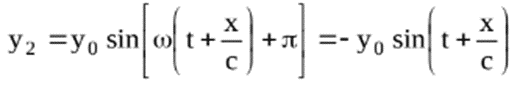



Коментари
Постави коментар